L’être humain a, à un moment de son évolution, ressenti le besoin de dénombrer les objets. Compter les baies, les mammouths, les pierres,… Il a alors utilisé ce qui lui tombait sous la main… et notamment ses doigts, tout comme le font encore les enfants aujourd’hui.
Cet art de compter avec les doigts s’appelle la dactylonomie
Certains peuples ont cependant été plus loin en utilisant, non pas uniquement leurs doigts, mais tout leur corps.
Je vous propose de faire un tour d’horizon de certaines méthodes de comptage, dont quelques-unes sont encore utilisées de nos jours.
Au sommaire de cet article:
Les techniques pour compter avec son corps, la description des différentes bases, une énigme, apprendre à multiplier avec les doigts, transformer des heures décimales en heures minutes et la solution de l’énigme

Les techniques
Faire correspondre “objet” à “doigt”
Pour nous, compter (avec ou sans les doigts) est aujourd’hui évident. Mais cela n’a pas toujours été le cas.
Il a fallu d’abord comprendre qu’on pouvait faire correspondre un objet à un caillou (ou à un doigt) par exemple et que le nombre de cailloux (ou de doigts) correspondait au nombre d’objets.

Ici, il y a autant de noisettes que de cailloux (ou que de doigts). Chaque noisette sera toujours reliée à un caillou (ou à un doigt) et à un seul. Et chaque caillou (ou chaque doigt) sera toujours relié à une noisette et une seule. On parle d’une correspondance un à un.
En mathématiques, lorsqu’on peut relier un à un chaque élément d’une collection (les noisettes) à chaque élément d’une autre collection (les cailloux), on dit que les collections sont en bijection ou qu’il existe une bijection entre les deux collections.
Si une collection de noisettes peut être mises en relation un à un avec une collection de cailloux, alors le nombre d’éléments dans chaque collection est identique. Il y a autant de noisettes que de cailloux.
On peut donc comparer deux collections, sans avoir besoin de connaître le nombre d’éléments de chaque collection, c’est-à-dire sans avoir besoin de savoir compter.

Ici on peut mettre en relation un à un, un certain nombres de fraises, mais pas toutes. On peut donc savoir qu’il y a plus de fraises que de noisettes.
Tout cela vous parait surement évident, mais ça ne l’était pas pour les premiers êtres humains à se lancer dans le décompte d’objets.
Regrouper pour compter
Lorsqu’il y a beaucoup d’objets, il est plus facile de les regrouper en tas d’un certain nombre.

Ici il y a le même nombre de bâtons à gauche et à droite. Mais il est beaucoup plus facile de les visualiser à droite, car regroupé en paquets de 5. On peut alors compter le nombre de paquets au lieu de compter les bâtons de manière individuelle.
On compte alors les unités (les bâtons individuels non regroupés) et les paquets (les bâtons regroupés par 5). Ici on a 5 paquets et 3 unités.
- Si on regroupe en paquets de 5, on dit qu’on va travailler en base 5.
- Si on regroupe en paquets de 10, on dit qu’on va travailler en base 10. C’est celle qu’on utilise en occident.
- Si on regroupe en paquets de 12, on dit qu’on va travailler en base 12.
- Si on regroupe en paquets de 20, on dit qu’on va travailler en base 20.
- Si on regroupe en paquets de 60, on dit qu’on va travailler en base 60.
Comment choisir la taille des paquets ?
La taille des paquets a été définie en fonction de la façon dont les différents peuples comptaient avec leur corps. D’une civilisation à l’autre, les méthodes de comptage et donc les tailles des paquets diffèrent.
En occident, nous utilisons la base 10.
Lorsqu’on a 10 unités, on a une dizaine. Lorsqu’on a 10 dizaines, on a une centaine, etc…
Pourtant certaines mesures ne suivent pas cette façon de regrouper les éléments. On a hérité des façons de faire plus anciennes. C’est ainsi que les heures fonctionnent par paquet de 12. Les minutes et secondes par paquet de 60.
Aperçu de différentes façons de compter avec son corps
Avec 10 doigts
En Occident, nous utilisons nos 10 doigts et nous pouvons compter jusqu’à 10. On dit qu’on compte en base 10, c’est-à-dire qu’on regroupe en paquet de 10.

Avec 10 doigts et 10 pieds
Certains peuples, comme les Mayas, les Aztèques, les Basques, les Esquimaux, utilisent leurs doigts et leurs orteils. Ils peuvent donc aller jusqu’à 20. On dit qu’ils comptent en base 20, c’est-à-dire qu’ils regroupent en paquet de 20. Il nous reste quelques traces de cette façon de compter, comme par exemple avec 80 (4 x 20).

Avec les 2 mains
Dans les régions d’Afrique et d’Océanie on trouve une technique qui permet de compter jusqu’à trente. On compte de un à cinq avec la main gauche, puis une fois le 5 atteint, on lève un doigt de la main droite, et on repart sur la main gauche pour compter de nouveau de 1 à 5. Lorsqu’on atteint de nouveau 5, on lève un 2ème doigt de la main droite, et ainsi de suite. On peut donc arriver à 25 à droite (5 doigts à 5) plus 5 à gauche, soit 30. On travaille ainsi en base 5, c’est-à-dire qu’on regroupe en paquet de 5.

Avec les phalanges des 10 doigts
D’autres civilisations utilisent les phalanges des doigts.
Le pouce de la main droite permet de se déplacer de phalange en phalange, en commençant par la première phalange de l’index, puis la deuxième, puis la troisième et ensuite en passant au doigt suivant, le majeur, 1ère phalange, 2ème, 3ème, puis annulaire, puis l’auriculaire.
Sur la main droite, on peut ainsi arriver à 12 (4 doigts à 3 phalanges). Une fois le 12 atteint, on met le pouce de la main gauche sur la première phalange de l’index et on recommence le décompte avec la main droite. Lorsqu’on atteint de nouveau 12 à droite, on déplace le pouce de la main gauche sur la 2ème phalange, etc…
On peut ainsi atteindre 144 (12 phalanges main gauche à 12 = 144) avec la main gauche plus 12 sur la main droite, soit 156 en tout. On compte ainsi en base 12, c’est-à-dire qu’on regroupe en paquet de 12. De cette base 12 il nous reste des douzaines d’œufs ou d’huitres, les douze heures sur les horloges, et les anciennes unités de mesure (1 pied = 12 pouces ; 1 pouce = 12 lignes et 1 ligne = 12 points) par exemple.
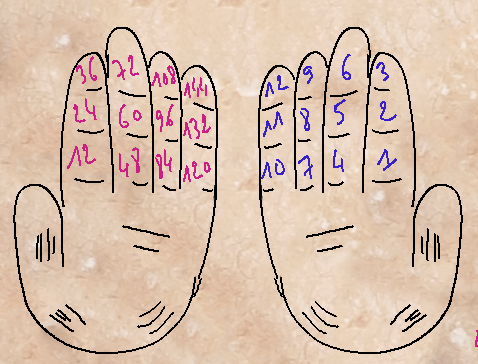
Une autre variante de la technique des phalanges a été utilisée par les Sumériens. Ils comptaient les phalanges avec la main droite, mais ils mémorisaient les retenus en pliant les doigts (et non plus en pointant les phalanges) de la main gauche. Ils arrivaient ainsi à 5 doigts à 12, soit 60. On dit qu’ils comptaient en base 60, c’est-à-dire qu’ils regroupaient en paquet de 60. Cette base 60 est utilisé pour le temps (60 secondes, 60 minutes) et pour les angles (360° = 6 x 60°).
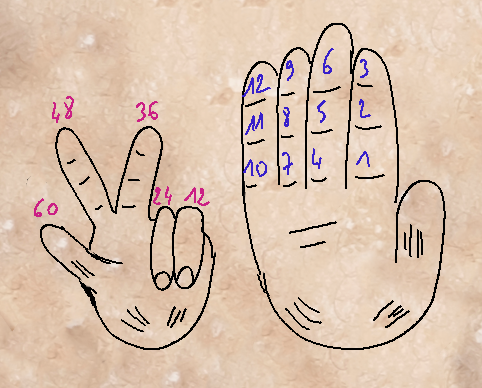
Description des différentes bases
Chiffres et nombres
Quelle différence y a-t-il entre un nombre et un chiffre.
Si on fait une analogie avec l’écriture, un chiffre est une lettre, un nombre est un mot.
Les lettres de l’alphabet a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y,z servent à former des mots comme table par exemple. Il y a 26 lettres dans l’alphabet français.
Les chiffres sont des signes ou des symboles qui permettent de composer des nombres.
Si on utilise les chiffres arabes et la base 10, on a 10 chiffres : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Ils servent à former des nombres comme 124 par exemple. Avec ces 10 chiffres, on peut écrire tous les nombres.
Si on utilise les chiffres romains, on a sept chiffres : I, V, X, L, C, D, M. Ils servent à écrire des nombres comme CXXIV (124) par exemple.
Tout comme il existe des mots à une seule lettre comme « à » par exemple, il existe des nombres à un seul chiffre comme « 8 » par exemple.
Zoom sur quelques bases
Base 10
On fait des paquets de 10. Les seuls chiffres utilisés sont donc le 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9.
Cette base est appelée base décimale.
Elle est utilisée pratiquement partout dans le monde, et c’est celle que vous utilisez couramment sans même y penser.

Les unités correspondent aux bâtons seuls qu’on ne peut pas regrouper en paquet de 10.
Les dizaines correspondent aux paquets de 10 bâtons.
Les centaines correspondent aux paquets de « 10 paquets de 10 »
Et ainsi de suite…
Base 5
On fait des paquets de 5. Les seuls chiffres utilisés sont donc le 0, 1, 2, 3 et 4.
Cette base est appelée base quinaire.
Elle est encore utilisée dans certaines régions du monde comme en Afrique (peul, serène…), en Amérique (nahuatl, otomi…), en Océanie (houailou, api…),ou en Asie (khmer).
Certaines langues utilisent ce système comme le wolof au Sénégal. On compte: un, deux, trois, quatre, cinq, puis cinq-un, cinq-deux, cinq-trois, cinq-quatre, dix, dix et un, dix et deux, etc.
Chez les Grecs anciens compter se disait cinquer, en rapport avec cette base qu’ils utilisaient.
À quoi correspond le nombre 342 ? Comment peut-on le convertir en base 10 (notre mode de calcul en occident) ?

342 veut dire 2 unités puis 4 paquets de 5, puis 3 paquets de « 5 paquets de 5 »
Base 12
On fait donc des paquets de 12.
Les chiffres arabes n’allant que de 0 à 9, on a ici besoin de 2 symboles supplémentaires. On utilise les deux premières lettres de l’alphabet, le A et le B, qui représentent respectivement 10 et 11.
Les seuls chiffres utilisés sont le 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A et B.
Cette base est appelée base duodécimale.
Les unités de mesures en Angleterre utilisent cette base.
À quoi correspond le nombre 36B ? Comment peut-on le convertir en base 10 (notre mode de calcul en occident) ?

Ici je n’ai pas représenté tous les bâtons faute de place. Imaginez que chaque rond noir contient 12 bâtons.
36B veut dire B unités (c’est-à-dire 11) puis 6 paquets de 12, puis 3 paquets de « 12 paquets de 12 »
Base 20
On fait donc des paquets de 20.
Les chiffres arabes n’allant que de 0 à 9, on a ici besoin de 10 symboles supplémentaires. On utilise les dix premières lettres de l’alphabet, du A au J, qui représentent respectivement de 10 à 19.
Les seuls chiffres utilisés sont le 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I et J
Cette base est appelée base vicésimale
Elle n’est plus utilisée, mais il en reste des vestiges, notamment dans le système français avec quatre-vingts (héritage celtique).
À quoi correspond le nombre A6I ? Comment peut-on le convertir en base 10 (notre mode de calcul en occident) ?

Ici je n’ai pas représenté tous les bâtons faute de place. Imaginez que chaque rond noir contient 20 bâtons, et que chaque rond vert contient 20 ronds noirs.
A6I veut dire I unités (c’est-à-dire 18) puis 6 paquets de 20, puis A paquets (c’est-à-dire 10) de « 20 paquets de 20 »
Base 60
On fait donc des paquets de 60. On utiliserait 60 chiffres pour écrire ces nombres.
Cette base est appelée base sexagésimale.
Elle est utilisée pour le temps, les angles… Elle a une origine babylonienne.
À quoi correspond le nombre 237 ? Comment peut-on le convertir en base 10 (notre mode de calcul en occident) ?

Ici je n’ai pas représenté tous les bâtons faute de place. Imaginez que chaque rond noir contient 60 bâtons, et que chaque rond vert contient 60 ronds noirs.
237 veut dire 7 unités puis 3 paquets de 60, puis 2 paquets de « 60 paquets de 60 »
Base 2
Cette base est un peu à part. En effet elle ne sert pas à compter. Elle a une origine plutôt « électrique », en indiquant si le courant passe ou si le courant ne passe pas.
Avec les bases 8 et 16, elle est utilisée en informatique et en électronique.
Le chiffre ici s’appelle un BIT.
Base 8
Elle s’utilise surtout en informatique pour représenter un nombre binaire de 8 bits, appelé l’octet (ou byte en anglais).
Aujourd’hui on lui préfère l’hexadécimale (base 16).
Base 16
On fait donc des paquets de 16.
Les chiffres arabes n’allant que de 0 à 9, on a ici besoin de 6 symboles supplémentaires. On utilise les six premières lettres de l’alphabet, le A, B, C, D, E et F, qui représentent respectivement 10, 11, 12, 13, 14 et 15.
Les seuls chiffres utilisés sont le 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E et F.
Cette base est appelée base hexadécimale.
Elle est utilisée en informatique. Avez-vous déjà travaillé avec un logiciel dans lequel vous pouvez choisir vos couleurs ? Je suis sûre que oui. Allez sur Word par exemple, Cliquer sur l’icône pour changer la couleur du texte, et choisissez autres couleurs, puis Personnalisées. Choisissez ensuite la couleur que vous voulez (en cliquant sur la couleur et en manipulant l’ascenseur)
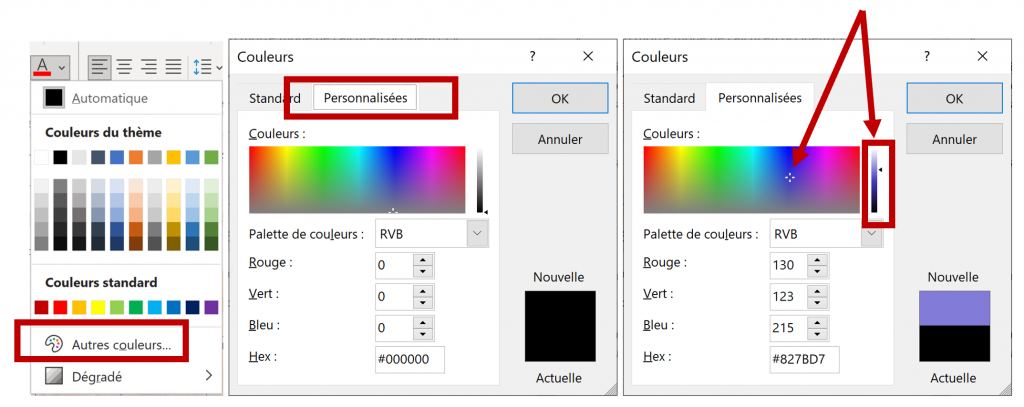
Word défini les couleurs en RVB (Rouge, Vert, Bleu) mais vous donne également le code Hex.
À quoi correspond ce code couleur ? C’est une façon de représenter les couleurs qui utilise la base hexadécimale. La couleur est notée # suivi du rouge puis du vert, puis du bleu. Pour chaque couleur de base (R V B), l’intensité est spécifiée par un entier hexadécimal qui va de 00 à FF.
Par exemple :

Si on veut un bleu pur, on va mettre le rouge à une intensité minimale, c’est-à-dire nulle, le vert également et le bleu à une intensité maximale, c’est-à-dire FF. On obtient le code #0000FF.
Si on veut un bleu « moins bleu », on va ajouter une nuance de vert, comme par exemple 99. Cela donne le code #0099FF.
Si je mélange du rouge intense avec du bleu intense, sans vert, on obtient du rose, avec le code #FF00FF.
En utilisant cette base, pour chaque teinte (R V B) on a 16×16 = 256 possibilités. Avec les 3 teintes mélangée, on arrive à créer
256x256x256=16 777 216 couleurs différentes.
À quoi correspond le nombre 1DA ? Comment peut-on le convertir en base 10 (notre mode de calcul en occident) ?

Ici je n’ai pas représenté tous les bâtons faute de place. Imaginez que chaque rond noir contient 12 bâtons.
1DA veut dire A unités (c’est-à-dire 10) puis D paquets (c’est-à-dire 13) de 16, puis 1 paquet de « 16 paquets de 16 »
Une énigme : Sur le marché de Umia

Dans une galaxie lointaine, très lointaine…
Non, il ne s’agit pas de Star Wars.
Notre histoire du jour se déroule sur la planète Umia. Celle-ci, et surtout sa capitale Yhin, est le centre de la civilisation galactique. Elle est notamment connue pour son marché, le plus grand de toutes les planètes connues et, donc, l’endroit où chacun est sûr de trouver ce qu’il cherche, y compris les denrées les plus rares. Ainsi, toutes les espèces s’y retrouvent en un grand mélange de formes, de couleurs, de coutumes et de langues.
Sur Umia, sans surprise, les formations de marchand sont les plus prisées. Et surtout les plus longues. En effet, chaque peuple a sa propre monnaie, et sa propre façon de compter. Chaque commerçant doit donc connaître les spécificités de tous les peuples qu’ils sont susceptibles de croiser, et il y en a beaucoup.
Laurenia est apprentie marchande, mais elle a encore du mal avec les différentes façons de compter. Originaire d’Yhin, elle compte en base 10, comme nous. Elle a pris des notes pour se souvenir quel peuple compte comment, mais a besoin d’aide pour convertir les valeurs.
Son premier client du jour provient de la planète Eiruta -ils sont reconnaissables à leur troisième œil sur le front- et lui commande « 2 grosses valeurs et 2 petites » de pommes. D’après ses notes, les eirutans comptent en base 20.
La suivante est très fine et très grande, aux cheveux faits de plantes, une sinnadienne à n’en pas douter. Les habitants de Sinnadus comptent en base 5. Celle-ci lui commande « 3 grosses et 4 petites » fraises.
Vient ensuite un couple originaire de Neerus. Leurs fourrures aux couleurs vives se remarquent de loin, ce sont d’ailleurs les seuls à la connaissance de Laurenia à ne pas mettre de vêtements. Ils réservent un gâteau pour « 2 grosses et 1 petite » personnes. Ce peuple compte en base 12.
En fin de journée, une personne emmitouflée dans une cape avec une capuche cachant son visage demande « 1 grosse et 5 petits » baies de sureau. L’emblème cousue sur le devant de son vêtement représente une guilde marchande basée à Balnore, dont la base officielle est la base 60.
A partir de ses notes de la journée, Laurenia doit transmettre à son maître les commandes qu’elle a prises, mais doit d’abord convertir les nombres en base 10. Pouvez-vous l’aider ?
Multiplier avec les doigts
Savez-vous qu’il est possible de faire des multiplications avec les doigts ?
Je vous propose ici 3 méthodes.
Vous pouvez suivre les explications en vous aidant de l’image. Je suis assez bonne en Maths mais pas au top en dessin, alors toutes mes excuses pour les doigts bizarres 😊 !
Multiplier 9 par un nombre compris entre 1 et 9
La méthode
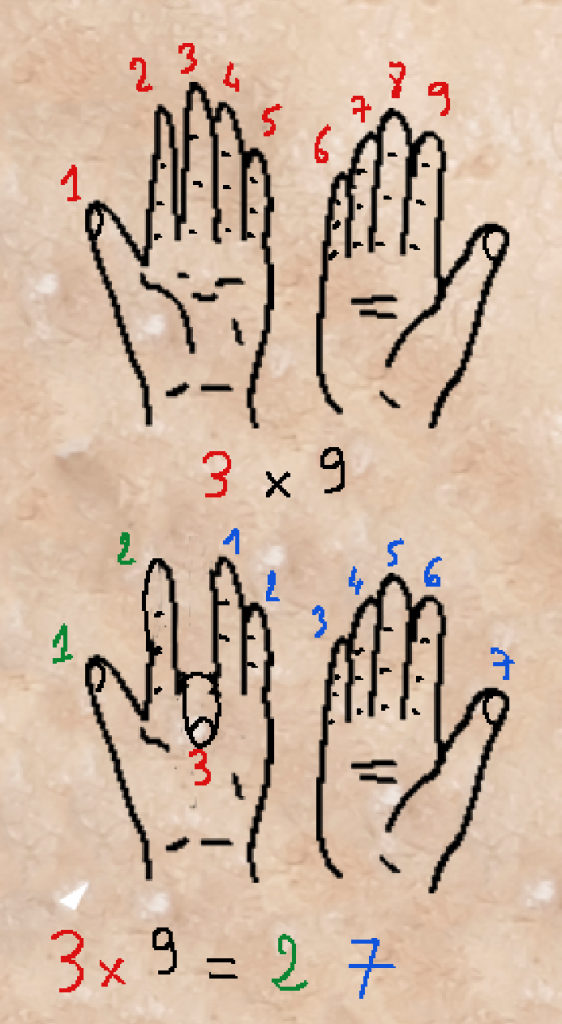
Méthode très simple, vous allez voir, vous devez seulement connaître votre gauche et votre droite :
Mettez vos mains à plat devant vous paume vers le haut. En partant de la gauche, vous avez le pouce, l’index, le majeur, l’annulaire, et l’auriculaire de la main gauche, puis l’auriculaire, l’annulaire, le majeur, l’index et le pouce de la main droite. Chaque doigt représente un chiffre, dans l’ordre de gauche à droite : 1, 2, 3, 4, 5, 6, 7, 8, 9 le pouce de la main droite n’a pas de chiffre attribué. Il sert juste pour lire le résultat.
Si vous voulez faire 3×9, vous allez plier le doigt correspondant au 3, c’est-à-dire le majeur de la main gauche. Pour obtenir le résultat de la multiplication, vous comptez le nombre de doigts à gauche du doigt plié, c’est le nombre des dizaines, et vous comptez le nombre de doigts à droite du doigt plié, c’est le nombre des unités. Ici il y a 2 doigts avant le majeur plié et 7 doigts à droite. Le résultat est donc 27. Et effectivement 3×9=27.
Magique, non ?
L’autre alternative est de connaître par cœur votre table du 9.
L’explication : Comment ça marche ?
9 x n = 10 x n – n
9 x n = 10 x n – n + 10 -10
9 x n = 10 x n – 10 + 10 – n
9 x n = 10 x (n – 1) + (10 – n)
(n – 1) représente les dizaines et (10 – n) représente les unités.
Quand on plie le doigt n, il y a (n – 1) doigts à gauche et (10 – n) doigts à droite.
Multiplier deux nombres compris entre 6 et 10
La méthode

Mettez vos mains à plat devant vous paume vers le haut.
En partant de la gauche, vous allez associer chaque doigt à un nombre.
Sur la main gauche et sur la main droite, le pouce est associé au 6, l’index au 7, le majeur au 8, l’annulaire au 9, et l’auriculaire de la main gauche au 10.
Si vous voulez faire 7×9, pliez sur la main gauche le doigt associé au 7 et tous les doigts situés à sa gauche. Donc vous allez plier le pouce (6), et l’index (7). Pliez ensuite sur la main droite le doigt associé au 9 et tous les doigts situés à sa droite. Ici vous allez plier le pouce (6), l’index (7), le majeur (8) et l’annulaire (9)
Pour obtenir le résultat, il faut comptez le nombre de doigts pliés pour obtenir les dizaines et il faut multiplier le nombre de doigts levés sur la main gauche par le nombre de doigts levés sur la main droite pour obtenir les unités.
Ici on a 2 doigts pliés à gauche et 4 doigts pliés à droite, soit 2+4=6 doigts, ce qui représente les dizaines.
On a 3 doigts levés à gauche et 1 doigt levé à droite, soit 3×1=3 doigts, ce qui représente les unités.
Notre résultat est donc 63. Or 7×9 est bien égal à 63.
Impressionnant, non ?
Mais là encore on est sensé connaitre les tables de multiplications jusque 10.
L’explication : Comment ça marche ?
Chaque nombre est compris entre 6 et 10, et donc peut s’écrire comme 5+quelque chose.
Sur la main gauche, on plie le nombre de doigts correspond à ce quelque chose. De même sur la main droite.
Il nous reste à gauche 5 moins ce quelque chose en doigts levé. De même à droite
Premier nombre : n = 5 + a
Deuxième nombre : m = 5 + b
Nombre de doigts pliés :
à gauche : a
à droite : b
Nombre de doigts levés :
à gauche : (5 – a)
à droite : ((5 – b)
Le produit de ces deux nombres donne :
(5 + a)(5 + b) = 25 + 5b + 5a + ab
La méthode nous dit que le chiffre des unités c’est (5 – a)(5 – b) (produit des doigts levés) et que le chiffre des dizaines c’est (a + b) (somme des doigts pliés). Vérifions que c’est juste. Notre résultat d’après la méthode vaut donc
10(a + b) + (5 – a)(5 – b) = 10a + 10b + 25 – 5b -5a + ab = 25 +5b + 5a + ab
On obtient bien la même chose.
Multiplier deux nombres compris entre 10 et 15
La méthode
Cette troisième astuce est plus utile, car on ne nous a jamais demandé d’apprendre les tables au-delà de 10 !
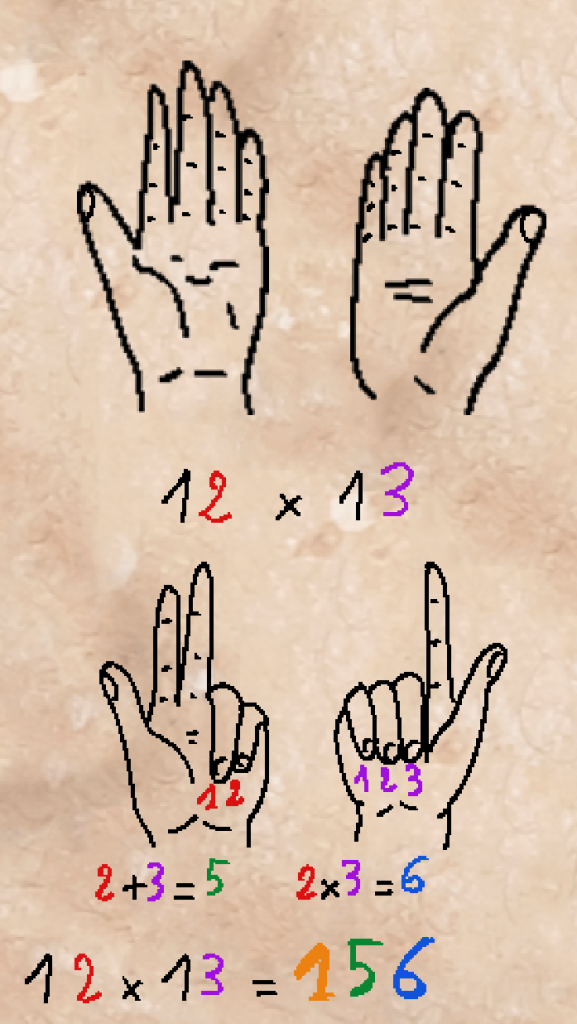
Alors comment faire très rapidement 12×13 sans calculatrice ?
Pour cette méthode, il n’est pas nécessaire de numéroter les doigts.
Il faut plier à gauche le nombre de doigts correspondant au nombre d’unité du premier nombre, ici 2.
Il faut plier à droite le nombre de doigts correspondant au nombre d’unité du deuxième nombre, ici 3.
Pour obtenir le résultat, on compte le nombre de doigts pliés au total. Cela nous donne le chiffre des dizaines.
On multiplie ensuite le nombre de doigts pliés à gauche par le nombre de doigt pliés à droite et cela nous donne le chiffre des unités.
On ajoute ensuite un 1 pour le chiffre des centaines.
Ici, on a 2 doigts pliés à gauche et 3 doigts pliés à droite, donc 2+3=5 doigts, ce qui représente les dizaines
Ici, on a 2 doigts pliés à gauche et 3 doigts pliés à droite, donc 2×3=6 doigts, ce qui représente les unités
Le résultat est donc 156. Je vous laisse vérifier avec la calculatrice. 12×13=156
Bluffant non ?
L’explication : Comment ça marche
Chaque nombre est compris entre 10 et 15, donc s’écrit sous la forme 10+quelque chose.
Sur la main gauche, on plie le nombre de doigts correspond à ce quelque chose. De même sur la main droite.
Premier nombre : n = 10 + a
Deuxième nombre : m = 10 + b
Le produit de ces deux nombres donne :
(10 + a)(10 + b) = 100 + 10b + 10 + ab = 100 + 10(a + b) + ab
Ce qui correspond bien à une centaine, (a + b) dizaine et a x b unités.
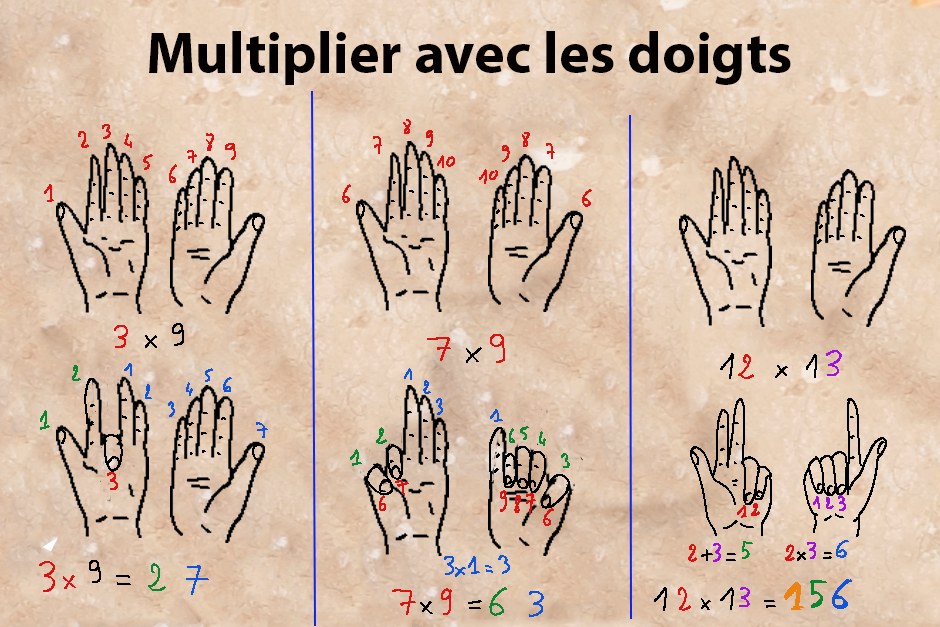
En résumé
Transformer des heures décimales en heures minutes et vice versa
Comment transformer des heures décimales (en base 10) en heures minutes (en base 60) ?
En effet les minutes et secondes se regroupent en paquet de 60. Elles se calculent en base 60, et non pas en base 10. Ce qui veut dire que 1h25 ne correspond pas à 1,25 heure !
Et à quoi cela peut bien servir de faire cette transformation ? Dès que vous voulez multiplier des heures par un taux horaire par exemple (pour le calcul de facture ou devis, ou pour le calcul de paie) vous devez convertir les heures en décimale.
Voyons la différence entre les heures minutes et secondes et les heures décimales.
Ce qu’il faut retenir c’est que 1h correspond à 60 minutes et que 1 minute correspond à 60 secondes. Ici on ne va pas mettre de secondes pour simplifier, et parce que c’est rare de mesurer un temps de travail à la seconde près !.
Pour transformer des heures (entières ou décimales) en minutes, on multiplie par 60. Si on prend 1h25, cela correspond à 1h entière, soit 1×60 = 60 minutes plus 25 minutes, soit au total 60+25=85 minutes. Si on prend 1,25 heures, on aura 1,25 x 60= 75 minutes. Vous avez une différence de 10 minutes !
C’est assez facile dans ce sens.
Dans l’autre sens, si vous voulez transformer des heures minutes en heures décimales, il faut d’abord tout mettre en minutes et ensuite se rappeler que 60 minutes = 1 heure et donc que 1 minute =1/60 heure.
Ainsi 1h25mn correspond à 85 minutes (on l’a calculé juste avant) et donc en heure décimale cela donne 85/60=1,42 heures (en arrondissant).
Automatiser ces calculs avec Excel
On peut utiliser Excel pour automatiser ces calculs. Dans ce cas, nous aurons besoin des fonctions suivantes : HEURE, MINUTE, QUOTIENT, MOD, TEMPS. Connaissez-vous ces fonctions ? Les avez-vous déjà utilisé ? Non ? Alors c’est l’occasion de les découvrir.
Je vous propose un tuto vidéo, et pour ceux qui n’aime pas la vidéo un tuto sous format pdf.
Tuto vidéo
Tuto pdf
Cliquez ici pour télécharger le pdf
Solution de l’énigme : Sur le marché de Umia
En base 20, on fait des tas de 20
2 grosses valeurs correspondent donc à 2 tas de 20, soit 40 pommes
2 petites valeurs correspondent à 2 unités, soit 2 pommes
Au total l’habitant de la planète Eiruta a commandé 42 pommes.
En base 5, on fait des tas de 5
3 grosses valeurs correspondent donc à 3 tas de 5, soit 15 fraises
4 petites valeurs correspondent à 4 unités, soit 4 fraises
Au total l’habitante de Sinnadus a commandé 19 fraises.
En base 12, on fait des tas de 12
2 grosses valeurs correspondent donc à 2 tas de 12, soit 24 personnes
1 petite valeur correspond à 1 unité, soit 1 personnes
Au total le couple de Neerus a commandé un gâteau pour 25 personnes
En base 60, on fait des tas de 60
1 grosse valeur correspond donc à 1 tas de 60, soit 60 baies de sureau
5 petites valeurs correspondent à 5 unités, soit 5 baies de sureau
Au total le marchand de Balnore a commandé 65 baies de sureau.





Ping : Humanité savante : A l’origine des maths | Cours Particuliers Professeurs Diplômés Primaire Collège Lycée